|Creative Engineering home page|

|Table of contents | Learning HighRoad | Using HighRoad| Reference|

| Previous |

 

Chapter 24 Technical information

 

This chapter outlines the methods of calculation used by HighRoad and describes some limits you need to be aware of.

 

Triangulation

The triangulation is constructed using the properties of a Voronoi diagram. A voronoi diagram consists of a set of polygons one for each point. The space enclosed by the polygon for a point is such that anywhere within the polygon is closer to point P than any other point. (Refer to Figure 24-1.)

 

Figure 24-1

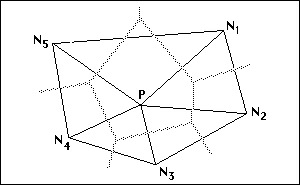
Each edge is associated with a link from point P to one of its neighbours N and the edge of the polygon is a perpendicular bisector of the link to the neighbour N. The triangulation is the set of all links corresponding to an edge on a voronoi polygon. You should verify that this correctly models the shape of the terrain particularly that no triangle edges cross linear features such as ridges, gullies, drainage ditches, kerb lines etc. If necessary you may have to insert a feature string as a breakline to correct the triangulation.


Earthworks

Method of calculating quantities

The volume of earthworks is calculated using the mean end area method. The area of cut and fill at each section at the nominated interval is calculated to the nearest square centimetre. The volume of cut (and fill) between two consecutive surveyed sections is calculated as the sum of the cut areas of the two sections multiplied by half the distance between the sections. The volume is calculated to the nearest 0.001 cubic metre.

 

Calculation of earthworks after stripping

Figure 24-2 shows the method used to allow for stripping before calculating quantities. The finished surface of the cut batter intersects with the natural surface. The natural surface is lowered by the depth of stripping between the points where the batter intersects the natural surface. The cut and fill volumes are then calculated.

 

Figure 24-2

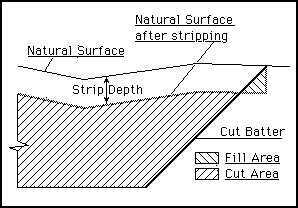
You can see that in the case of a cross section which is totally in cut, a very small quantity of fill will be calculated in the area below the cut batter and down to the stripped surface. The cut batter is shown with no surface treatment in Figure 24-2. In cases where there is a layer of topsoil on the cut batters, the earthworks would be calculated to the underside of the topsoil layer. If the depth of topsoil on the batter is equal to greater than the depth of stripping, the section would be totally in cut.

 

Allowance for surface layer thickness

When calculating quantities, HighRoad allows for the thickness of the surface layers. The cut and fill volumes are calculated between the underside of the surface layers and the natural surface stripped of topsoil. This is shown in Figure 24-3.

 

Figure 24-3

 

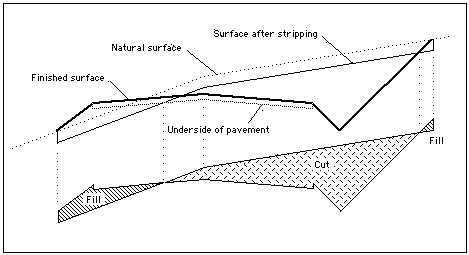
Allowance for bulking or compaction

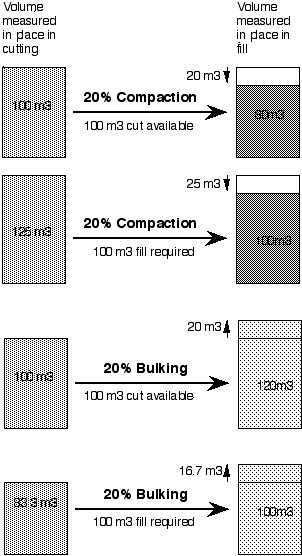
Consider the case where the volume of earth from a cutting occupies less volume after it is placed and compacted in a fill. If 100 m3 of earth from the cutting (measured in place) occupies 80 m3 when it is compacted into a fill (again measured in place), this would be specified as 20% compaction. The volume changes by a factor of 0.8 from cut to fill.

When calculating cut to fill, HighRoad takes into account compaction or bulking. Continuing with this example, that is, a compaction factor of 0.8, if the road had a cut volume of 100 m3 and a fill volume of 80 m3, this would be listed as:

100 m3 of cut to fill.

 


Figure 24-4

There would be no cut to spoil or borrow to fill, that is no excess cut to dispose of, or excess fill to bring onto the job.

If there was 100 m3 of fill required in this road, HighRoad calculates the amount of cut required for this fill by dividing the volume of fill by the compaction factor. In this case, the volume of cut (measured in place) required for a 100 m3 fill is:

100/0.8 = 125 m3.

As there is only 100 m3 of cut available, an additional 25 m3 would be required. This would be listed as:

100 m3 cut to fill

25 m3 borrow to fill.

 

Note: These calculations make no allowance for the volume occupied by the earth during transport. The volume occupied by 100 m3 of earth from cutting may increase by 30% when it is loose while being hauled. If you wish to estimate the loose volume for haulage you must take account of this separately.

Figure 24-4 shows diagrams of 20% compaction and 20% bulking for the case where 100 m3 of cut is available and 100  m3 of fill is required.

 

Restrictions

Maximum distance between offsets

The maximum distance allowed between consecutive offsets on a cross section is 1000 m. The maximum difference between consecutive elevations is 100 m. There is currently no range checking in place to ensure that these criteria are met. If your design exceeds these values, errors in the calculation of earthworks volumes and in the drawing of cross sections may occur.

 

Maximum length of road

The maximum length of road that can be designed is 32 km. (This length is controlled by the maximum value of the horizontal scroll bar.)

 

 

Maximum number of survey points

The maximum number of survey points is limited only by the memory of your computer. A project of 5,000 to 10,000 points will be approximately one megabyte in size. The exact amount varies depending on how much memory is used up by requirements for typical sections and profiles etc. There are two types of terrain model data formats used internally by HighRoad. When creating a new project you have the option of choosing Large format which allows terrain models with greater than 65000 points. This large format is not compatible with versions of HighRoad prior to version 5.0. The maximum number of points is also limited by how many Points modules you are licensed to use. These increase increase by 10 times for each Points module.

 

Calculations

Method of interpolation between typical sections

Wherever there is a gap between typical sections, HighRoad interpolates between these two sections. The offset and the crossfall are interpolated linearly between the two sections. For example, if Typical Section 1 applies to chainage 100.000 and Typical Section 2 applies from chainage 200.000, interpolation will be applied in the range 100.000 to 200.000. Consider a typical section at chainage 125.000. The link to be interpolated has an offset of 4 m and crossfall of 0% at chainage 100.000, and an offset of 8 m and crossfall of 4% at chainage 200.000. The interpolation would be calculated as follows:

offset at 125 = 4 + (8 - 4) x (125.000 - 100.000) = 5 m

(200.000 - 100.000)

crossfall at 125 = 0 + (4 - 0) x (125.000 - 100.000) = 1%

(200.000 - 100.000)

 

The surface and edge types for the interpolated section are taken from the first typical section. If the surface or edge type changes from one section to the next, the change is not applied until the start of the next section.

 

Mathematical basis of all calculations

HighRoad uses integer arithmetic for most calculations. Integer arithmetic is used primarily for speed. The integers used are mostly 32 bit, with occasional use of 64 bit integers for some intermediate calculations. The use of 32 bit integers limits the maximum number that can be used to ± 2,147,483,647, which is ample for most calculations.

The maximum chainage that can be used is currently limited to 999,999.999 m. The use of integer arithmetic does place some limits on the maximum difference between offsets on a cross section. Offsets on a cross section cannot be more than 1000 m apart and the distance between consecutive elevations cannot be more than 100 m.

Plan drawing uses floating point arithmetic for the calculation of co-ordinates.

| Previous |